Trigonometría: ¿Cuáles son las ecuaciones que describen cada tipo de movimiento?

Movimiento Rectilíneo

Sabemos que la velocidad V es constante; esto significa que no existe aceleración.La posición S en cualquier instante t viene dada por S=VT. Otra fórmula muy importante es: X=X0 + V(t-t0)

Movimiento ondulatorio

Hay distintos tipos de ondas y distintos niveles de conocimientos en los que puede responderse tu pregunta. Te cuento acerca del caso mas simple, que son las ondas armónicas (cuya forma puede describirse mediante funciones seno o coseno). Estas ondas tienen tres parámetros que las determinan: Amplitud: Que es el máximo valor de energía que pueden tomar. Frecuencia: La cantidad de veces por segundo en que la onda alcanza un valor dado de energía. Fase: Determina el valor de energía en un instante inicial; este parámetro es de interés según la aplicación.La forma matemática es: A x Seno (2 x PI x F + P)Siendo A la amplitud, PI=180°, F la frecuencia y P la fase.

Movimiento circular

En el estudio del movimiento circular uniforme hemos visto la velocidad del móvil no cambia de módulo pero cambia constantemente de dirección. El móvil tiene una aceleración que está dirigida hacia el centro de la trayectoria, denominada aceleración normal y cuyo módulo es

Movimiento Parabólico

${\mathbf {v_{0}}}=v_{0}\,\cos {\phi }\,{\mathbf {i}}+v_{0}\,\sin {\phi }\,{\mathbf {j}}$ 2.0

${\mathbf {a}}=-g\,{\mathbf {j}}$

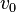donde: $v_{0}\,$ es el módulo de la velocidad inicial. $\phi \,$ es el ángulo de la velocidad inicial sobre la horizontal. $g\,$ es la aceleración de la gravedad. ${\mathbf {i}},{\mathbf {j}}$ son dos ver sores (vectores unitarios) en el plano.La velocidad inicial se compone de dos partes: $v_{0}\,\cos {\phi }$ que se denomina componente horizontal de la velocidad inicial.En lo sucesivo $v_{{0x}}\,$ $v_{0}\,\sin {\phi }$ que se denomina componente vertical de la velocidad inicial.En lo sucesivo $v_{{0y}}\,$ Se puede expresar la velocidad inicial de este modo: ${\mathbf {v_{0}}}=v_{{0x}}\,{\mathbf {i}}+v_{{0y}}\,{\mathbf {j}}$ Será la que se utilice, excepto en los casos en los que deba tenerse en cuenta el ángulo de la velocidad inicial.

Movimiento oscilatorio

(2) $\frac{d^2x}{dt^2} = a(t) = -\omega^2x$
La solución de la ecuación diferencial (2) puede escribirse en la forma

Movimiento parabólico

Hay dos ecuaciones que rigen el movimiento parabólico:

Siendo $m\,$ la masa del cuerpo en desplazamiento. Escribiendo $\scriptstyle \omega^{2} = k/m$ se obtiene la siguiente ecuación donde $\omega$ es la frecuencia angular del movimiento:

(3) $x(t) = A \cos(\omega t + \phi)\,$

donde: $x\,$ es la elongación o desplazamiento respecto al punto de equilibrio. $A\,$ es la amplitud del movimiento (elongación máxima). $\omega\,$ es la frecuencia angular $t\,$ es el tiempo. $\phi\,$ es la fase inicial e indica el estado de oscilación o vibración (o fase) en el instante t = 0 de la partícula que oscila.Además, la frecuencia de oscilación puede escribirse como esto:(4) $f = \frac{\omega}{2 \pi} = \frac{1}{2 \pi} \sqrt{\frac{k}{m}}$ , y por lo tanto el periodo como $T = \frac{1}{f} = \frac{2 \pi}{\omega} = 2 \pi \sqrt{\frac{m}{k}}$ La velocidad y aceleración de la partícula pueden obtenerse derivando respecto del tiempo la expresión $x(t) = A \cos(\omega t + \phi)\,$ .

Trigonometría

lunes, 24 de febrero de 2014

¿Cuáles son las ecuaciones que describen cada tipo de movimiento?

Movimiento oscilatorio

(2) $\frac{d^2x}{dt^2} = a(t) = -\omega^2x$
La solución de la ecuación diferencial (2) puede escribirse en la forma

Siendo $m\,$ la masa del cuerpo en desplazamiento. Escribiendo $\scriptstyle \omega^{2} = k/m$ se obtiene la siguiente ecuación donde $\omega$ es la frecuencia angular del movimiento:

No hay comentarios:

Publicar un comentario

Temas

lunes, 24 de febrero de 2014

¿Cuáles son las ecuaciones que describen cada tipo de movimiento?

Movimiento oscilatorio (2)La solución de la ecuación diferencial (2) puede escribirse en la forma

Siendo la masa del cuerpo en desplazamiento. Escribiendo 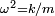se obtiene la siguiente ecuación donde es la frecuencia angular del movimiento:

No hay comentarios:

Publicar un comentario

Movimiento oscilatorio

(2) $\frac{d^2x}{dt^2} = a(t) = -\omega^2x$
La solución de la ecuación diferencial (2) puede escribirse en la forma

Siendo $m\,$ la masa del cuerpo en desplazamiento. Escribiendo $\scriptstyle \omega^{2} = k/m$ se obtiene la siguiente ecuación donde $\omega$ es la frecuencia angular del movimiento: